A piecewise function is a function which is defined by multiple subfunctions, each subfunction applying to a certain interval of the main function's domain (a subdomain). Piecewise is actually a way of expressing the function, rather than a characteristic of the function itself, but with additional qualification, it can describe the nature of the function. For example, a piecewise polynomial functions: a function that is a polynomial on each of its subdomains, but possibly a different one on each.
Note that, in this case, we have three different “formulas” for f(x): -x + 1, 2 and x2- 4. But remember, with a function, when you evaluate f(x), you should get ONE ANSWER—not three. Otherwise, you don’t have a function.
Note that, in this case, we have three different “formulas” for f(x): -x + 1, 2 and x2- 4. But remember, with a function, when you evaluate f(x), you should get ONE ANSWER—not three. Otherwise, you don’t have a function.
How do you know which answer you should have
(i.e., which formula you should use)? The “formula” is chosen using the
right-side of the piecewise-defined function (the “if …” part).
For example, suppose we wanted to find f( − 3).
Since − 3
< − 1, we will use the first “formula”:
f( − 3)
= - (-3) +1 = 4.
If we want to find f(5),
since 5 > 3,
we use the third “formula”:
f(5)
= 52 - 4 = 21.
What about finding f(1)?
Note that in the interval (-1,3) the value of function is 2.
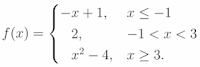

No comments:
Post a Comment